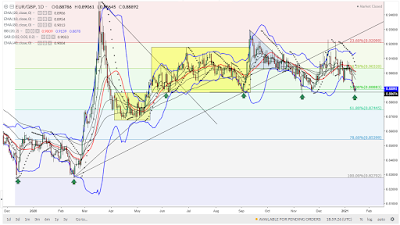
At a glance, we can notice that the cross is in a trading range (see the yellow rectangle), between 0.72 and 0.727. Those levels are also respectively the 38.20% FIBO level and 50% FIBO level, of a set-up top-bottom 0.755 and 0.70. The 50% FIBO level represents also the upper level of the previous gap-down (see the yellow ellipse).
In this way, the mentioned price levels are very important because they are redundant. Some useful trading strategies should be the following:
1) a short set-up from top to bottom (in the trading range, 0.727-0.72);
2) a long set-up from bottom to top (in the trading range, 0.72-0.727);
3) a short set-up of a wider scope, with a longer time frame, outside the rectangle; in other words, short at the break of 0.72, with confirmations and targets the lower FIBO levels, before 0.712, then 0.70;
4) a long set-up of a wider scope, with a longer time frame, outside the rectangle; in other words, long at the break of 0.727, with confirmations and targets the upper FIBO levels, before 0.733, then 0.743.
With this chart framework, the rectangle (or trading range) is the real focus: so, it is very important to look at it, in order to build our trading strategy, in one direction or another.
The following chart is explicative, of course.
 |
| Chart from Markets.com |
If we change the time frame, with a 4H chart, the view is the same.
The chart shows the multiple tests of the cross, at the tops of the rectangle. The tests are highlighted also by other indicators and oscillators, like RSI, CCI, and Williams %R.
The cross is in the overbought area: +100 for CCI, -20 for Williams %R, and +70 for RSI. This should represent a trend change (from an uptrend to a downtrend, from overbought area to oversold area) if the confirmations will occur, as previously said. At the moment it could be just a movement included in the trading range and a repulsion area with the tops of the rectangle as a resistance area.
The same thing is valuable in the hypothesis of the uptrend continuation (and not a reversal, in this way), with the break of the mentioned resistance area.
To conclude, let's keep focused on the rectangle and on its levels, also if we look at the candlesticks chart: there are a lot of Doji candles and candles with large shadows; they represent a lack of trend, for the moment and otherwise, they are the symbol of a real trading range area.
 |
| Chart from Markets.com |